01 知识表达与推理
- 逻辑与推理是人工智能的核心问题
- 符号主义人工智能方法基于如下假设:可通过逻辑方法来对符号及其关系进行计算,实现逻辑推理,辨析符号所描述内容是否正确。
- 以符号主义为核心的逻辑推理:将概念 (如命题等) 符号化,从若干判断 (前提) 出发得到新判断 (结论)(从知识到知识的过程)
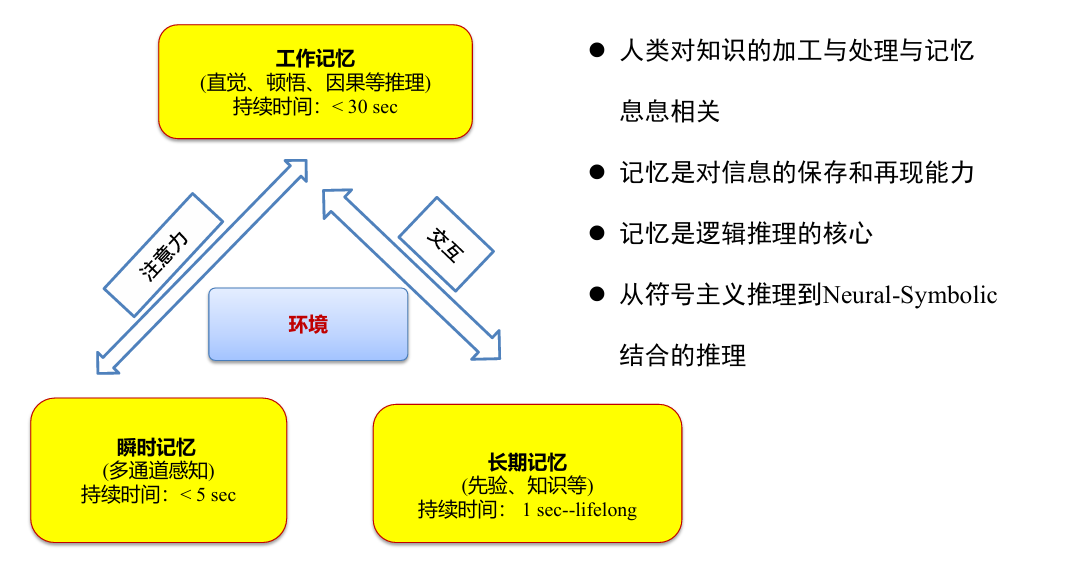
对记忆的理解:
01 命题逻辑
命题
命题:一个能确定为真或为假的陈述句
- 用小写符号来表示,如 p 或者 q
- 总有一个“值”,称为真值:为真 True 或为假 False
- 无法判断真假的描述性句子都不能作为命题

分类
- 原子命题:简单命题,不包含其他命题作为其组成部分的命题
- 符合命题:包含其他命题作为其组成部分的命题
- 可通过命题联结词 (connectives)对已有命题进行组合,得到新命题
| 命题连接符号 | 表示形式 | 意义 |
|---|---|---|
| 与 (and) | 命题合取 (conjunction),即“ |
|
| 或 (or) | 命题析取 (disjunction),即“ |
|
| 非(not) | 命题否定 (negation),即“非 |
|
| 条件 (conditional) | 命题蕴含 (implication),即“如果 |
|
| 双向条件 (bi-conditional) | 命题双向蕴含 (bi-implication),即“ |
逻辑等价:给定命题
| 逻辑等价的例子 | |
|---|---|
推理规则
推理是按照某种策略从前提出发推出结论的过程
| 推理规则的例子 | |
|---|---|
| 假言推理 (Modus Ponens) |
|
| 与消解 (And-Elimination) |
|
| 与导入 (And-Introduction) |
|
| 双重否定 (Double-Negation Elimination) | |
| 单项消解或单项归结 (Unit Resolution) | |
| 消解或归结 (Resolution) |
范式 (normal form):把命题公式化归为一种标准的形式
- 有限个简单合取式构成的析取式称为析取范式
- 假设
为简单的合取式,则 为析取范式
- 假设
- 有限个简单析取式构成的合取式称为合取范式
- 假设
为简单的析取式,则 为合取范式
- 假设
任一命题公式都存在着与之等值的析取范式与合取范式,但命题公式的析取范式与合取范式都不是唯一的

02 谓词逻辑
命题逻辑的局限性:在命题逻辑中,每个陈述句是最基本的单位 (即原子命题),无法对原子命题进行分解
- 不能表达局部与整体、一般与个别的关系
谓词逻辑:将原子命题进一步细化,分解出个体、谓词 predicate 和量词 quantifier
- 个体:所研究领域中可以独立存在的具体或抽象的概念
- 谓词:刻画个体属性或者描述个体之间关系存在性的元素,其值为真或为假
个体与谓词
例如,𝑃(𝑥) 表示:
- 𝑃是谓词, 𝑥是个体,𝑥被称为变量,其具体取值叫个体常项
- 函数是从定义域到值域的映射
- 谓词是从定义域到{True, False}的映射
- Richard 是国王。
- King (Richard)
- 其中,Richard 是一个个体常量,King 是一个描述“国王”这个一元关系的谓词
- Lucy 和 Lily 是姐妹
- Sister (Lucy, Lily)
- 其中,Lucy 和 Lily 是两个个体常量,Sitter 是一个描述“姐妹” 这个二元关系的谓词
量词
量词
- 全称量词 (universalquantifier, ∀)
- ∀𝑥表示定义域中的所有个体,∀𝑥𝑃(𝑥) 表示定义域中的所有个体具有性质 P
- 存在量词 (existentialquantifier, ∃)
- ∃𝑥表示定义域中存在一个或若干个个体,∃𝑥𝑃(𝑥) 表示定义域中存在一个个体或若干个体具有性质 P
量词之间的逻辑等价关系
变元
- 约束变元在全称量词或存在量词的约束条件下的变量符号
- 自由变元:不受全称量词或存在量词约束的变量符号
相关的逻辑等价关系:
- A (x) 是包含变元 x 的公式,B 是不包含变元 x 的谓词公式
- A (x) 和 B (x) 是包含变元 x 的谓词公式
- 若多个量词都是全称量词或者都是存在量词,则量词的位置可以互换;若多个量词中既有全称量词又有存在量词,则量词的位置不可以随意互换
设 A (x, y) 是包含变元 x y 的谓词公式:
设
- 全称量词消去 (Universal Instantiation, UI):
- 全称量词引入 (Universal Generalization, UG)
- 存在量词消去 (Existential Instantiation, EI):
- 存在量词引入 (Existential Generalization, EG):
例 2.12 已知:
试证明:(
证明过程:
(已知) (已知) (2 的 EI) (1 的 UI) (由 3 知) (4 和 5 的假言推理) (由 3 知) (由 6 知) (7 和 8 的合取) (9 的 EG)
项、原子公式与合式公式
项、原子谓词公式、合式公式
- 项:描述对象的逻辑表达式
- 常量符号和变量符号是项
- 若
是 元函数符号, 是项,则 是项 - 有限次数地使用上述规则产生的符号串是项
- 原子谓词公式
- 若
是 元谓词, 是项,则称 是原子谓词公式
- 若
- 合式公式:由逻辑联结词和原子公式构成的用于陈述事实的复杂语句,又称谓词公式
- 命题常项、命题变项、原子谓词公式是合式公式
- 如果
是合式公式,则 也是合式公式 - 如果
和 是合式公式,则 、 、 都是合式公式 - 如果
是合式公式, 是个体变项,则 和 也是合式公式 - 有限次数地使用上述规则构成的表达式是合式公式
例 2.14 前提:1) 每驾飞机或者停在地面或者飞在天空;2) 并非每驾飞机都飞在天空
结论:有些飞机停在地面
形式化:plane
已知:
请证明:(
证明:
von_fly (已知) V on_fly von_fly
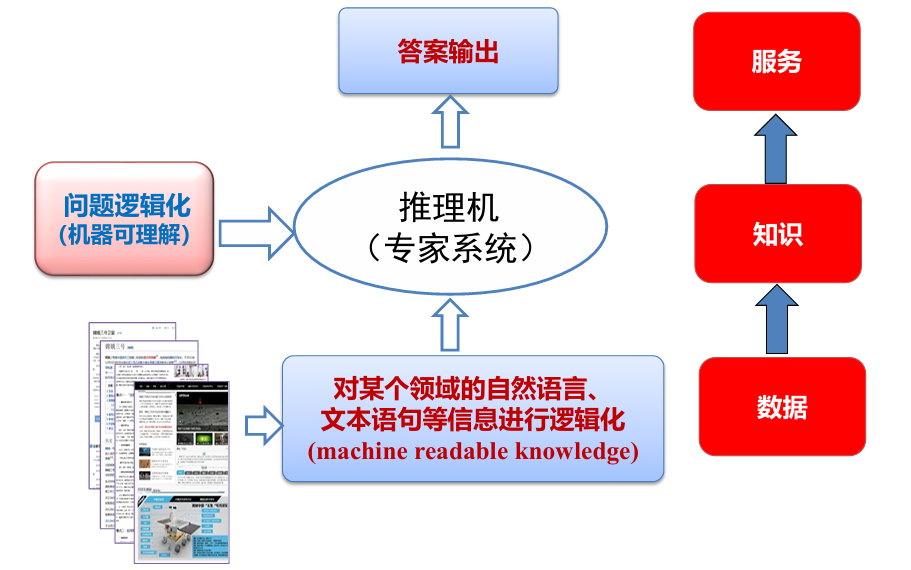
03 知识图谱推理
基本概念
知识图谱
- 包含多种关系的图
- 每个节点是一个实体,如人名、地名、事件和活动等
- 任意两个节点之间的边表示这两个节点之间存在的关系
- 任意两个相连节点及其连接边表示成一个三元组(triplet), 即 (left_node, relation, right_node)
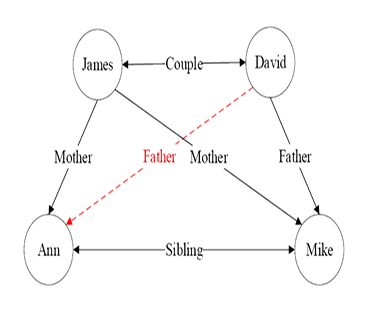
现在面临一个问题,如何从知识图谱中推理得到:father (David, Ann) ?
- 从具体例子中学习如下规则
归纳逻辑程序设计 (inductive logic programming,ILP) 算法
ILP:使用一阶谓词逻辑进行知识表示,通过修改和扩充逻辑表达式对现有知识归纳,完成推理任务
- 代表性方法:一阶归纳学习 FOIL(First Order Inductive Learner)
- 通过序贯覆盖实现规则推理
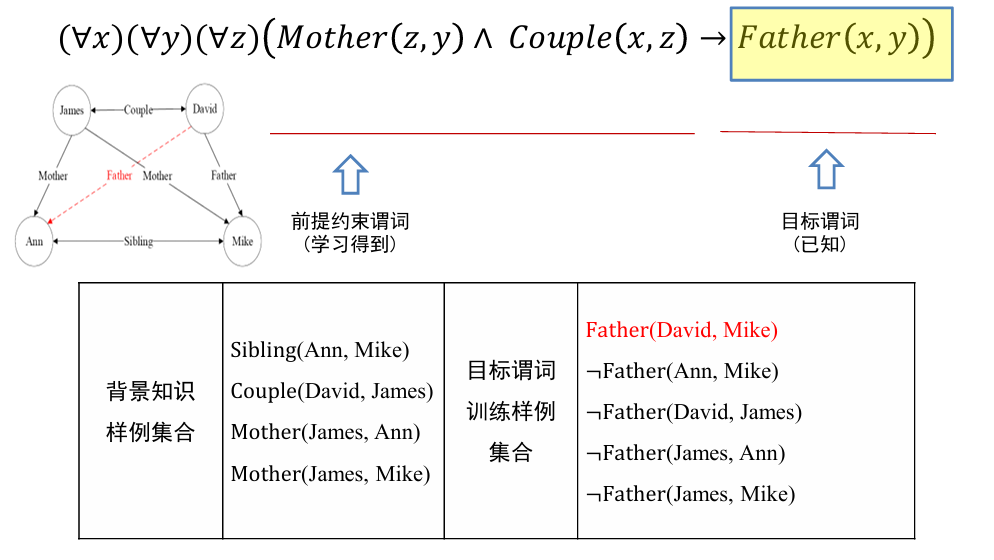
对于:
- 前提约束谓词:我们通过学习得到
- 目标谓词:已知
FOIL 算法
- 输入:目标谓词 P, P 的训练样例(正例集合 E+和反例集合 E-),其他背景知识
- 输出:推导得到目标谓词
的推理规则 - 流程
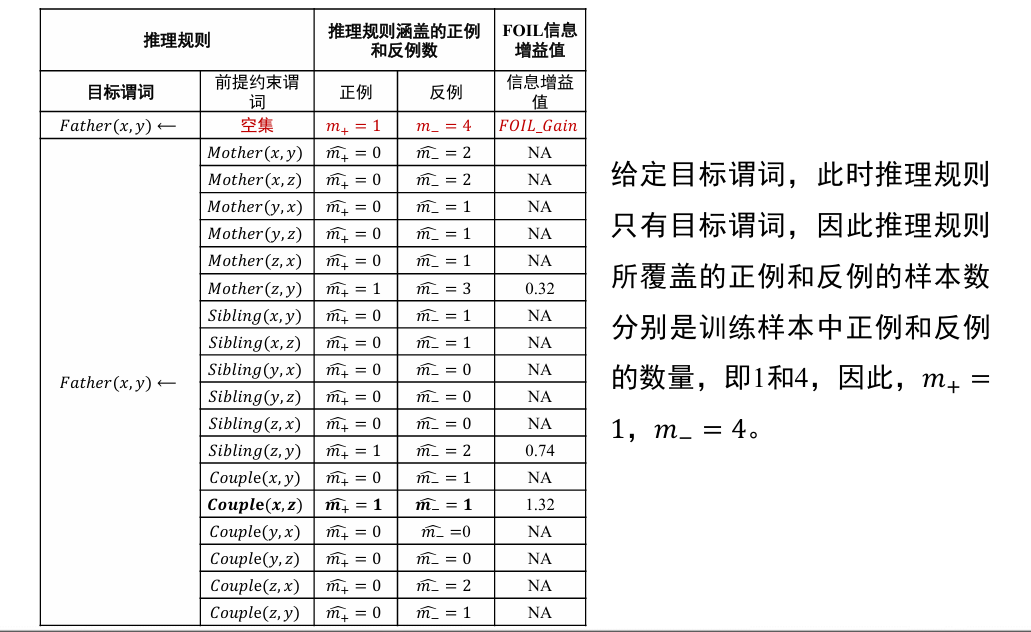
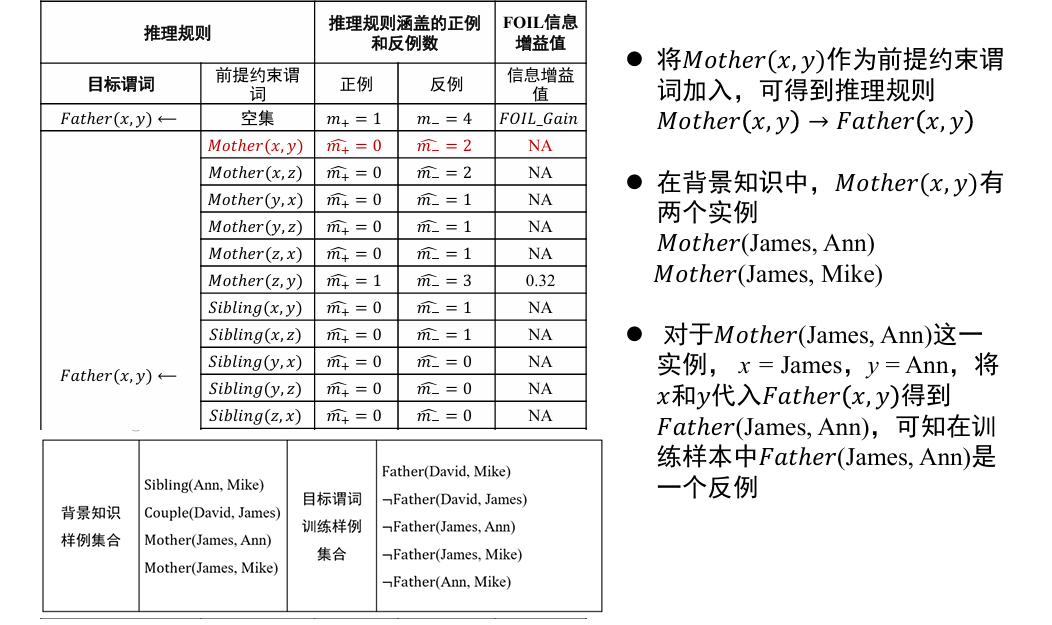
- 将目标谓词作为所学习推理规则的结论
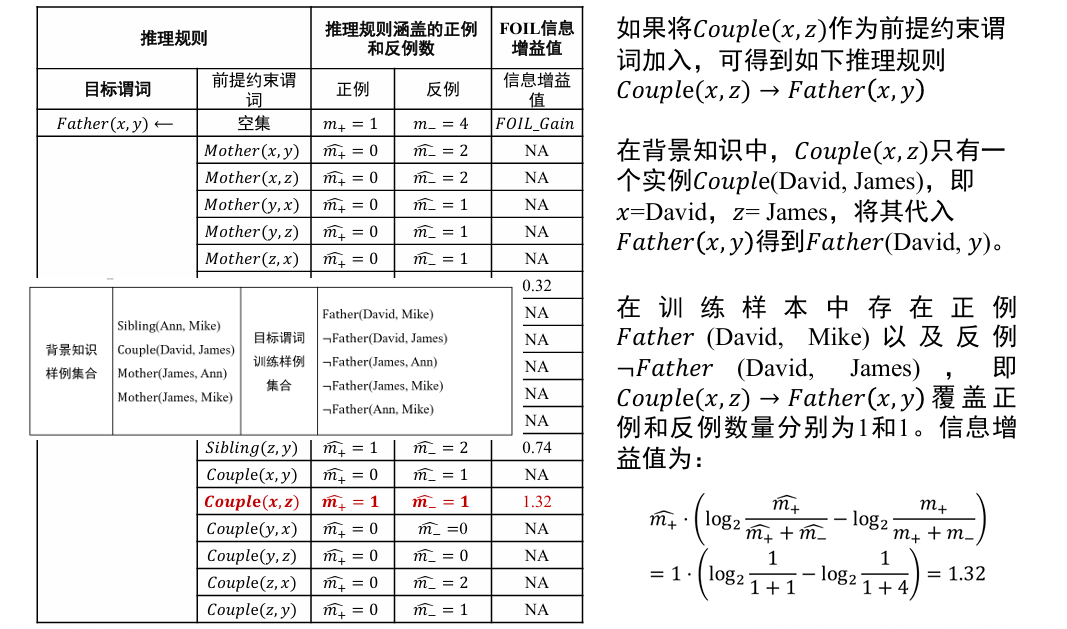
- 将其他谓词逐一作为前提约束谓词加入推理规则,计算所得到推理规则的 FOIL 信息增益值,选取最优前提约束谓词以生成新推理规则,并将训练样例集合中与该推理规则不符的样例去掉
- 重复 2 过程,直到所得到的推理规则不覆盖任意反例
哪些谓词好呢? 可以作为目标谓词的前提约束谓词?
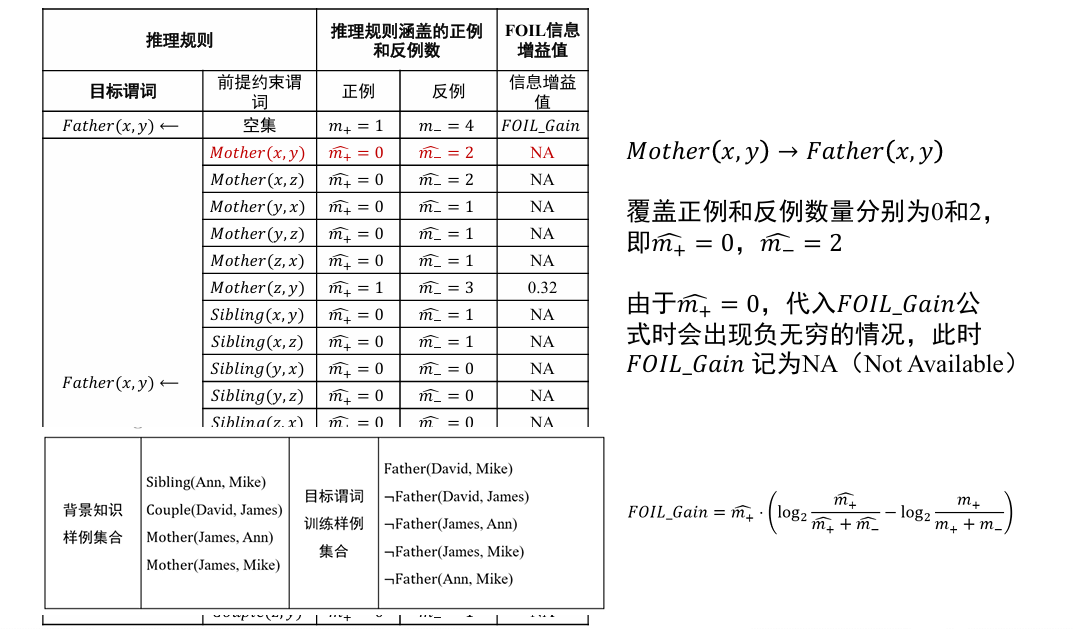
- 通过 FOIL 中的信息增益值来衡量
- 其中,
和 是增加前提约束谓词后所得新推理规则覆盖的正例和反例的数量, 和 是原推理规则所覆盖的正例和反例数量

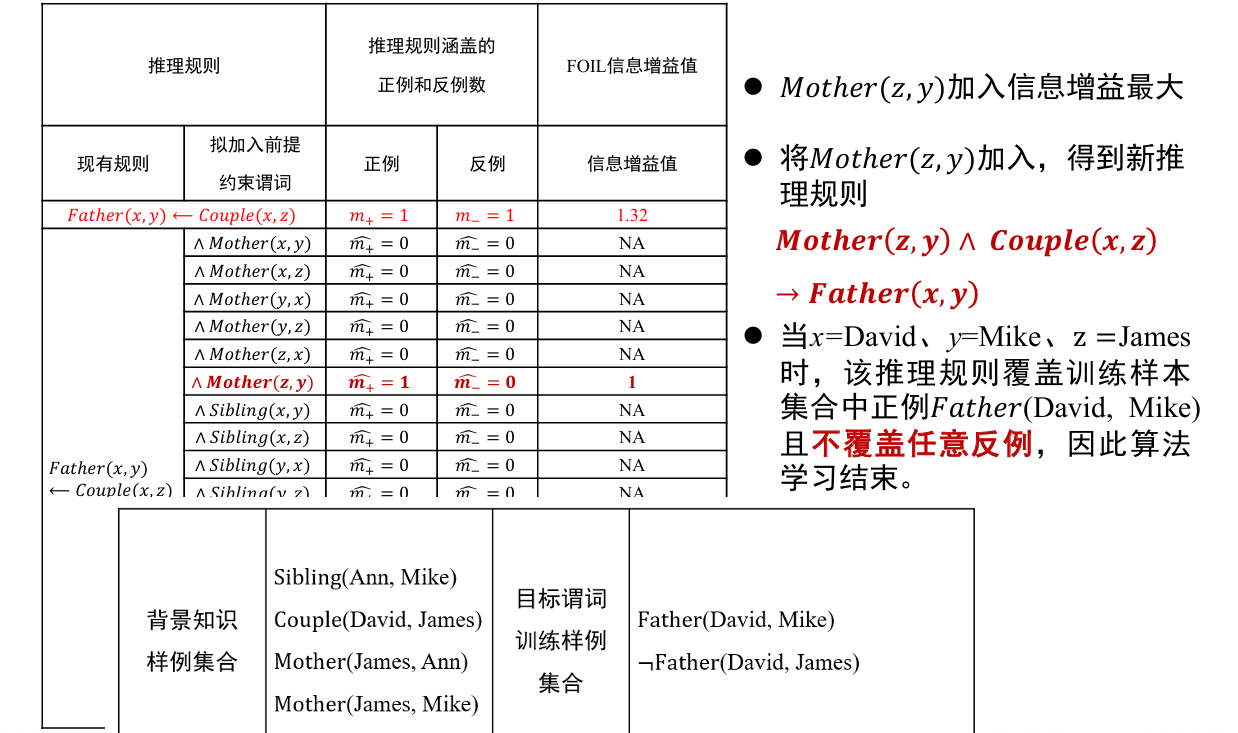
路径排序算法(path ranking algorithm, PRA)
路径排序推理算法(PRA)的基本思想:将实体之间的关联路径作为特征,来学习目标关系的分类器,可以分为如下三步:
- 特征抽取:生成并选择路径特征
的集合 - 生成路径的方式有随机游走 (random walk)、广度优先搜索、深度优先搜索等
- 特征计算:计算每个训练样例的特征值
- 特征值表示从实体节点 s 出发,通过关系路径
到达实体节点 的概率 - 也可以表示为布尔值,表示实体 s 到实体
之间是否存在路径 - 还可以是实体 s 和实体
之间路径出现频次、频率等
- 特征值表示从实体节点 s 出发,通过关系路径
- 分类器训练:根据训练样例的特征值,为目标关系训练分类器。当训练好分类器后,即可将该分类器用于推理两个实体之间是否存在目标关系
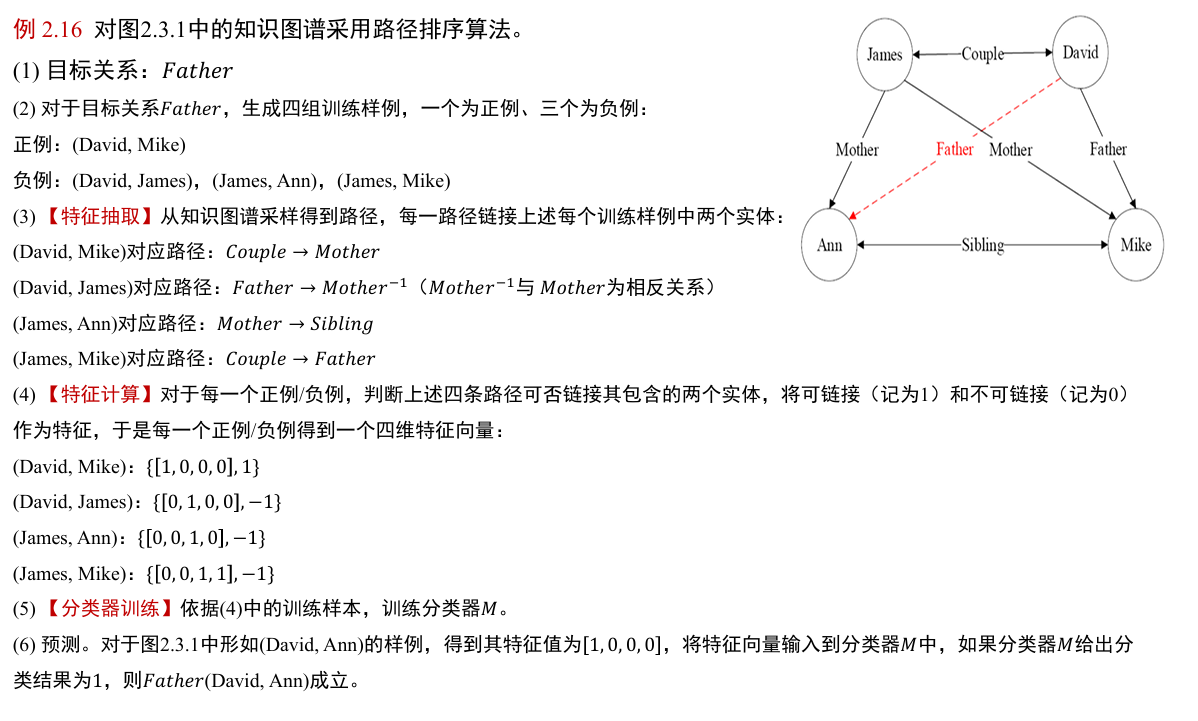
基于分布式表示的知识推理
将知识图谱中的节点和节点之间的关系均映射到连续数值空间中 (即分布式表示), 同时对映射过程进行约束,使得知识图谱中节点之间的拓扑结构得以保留
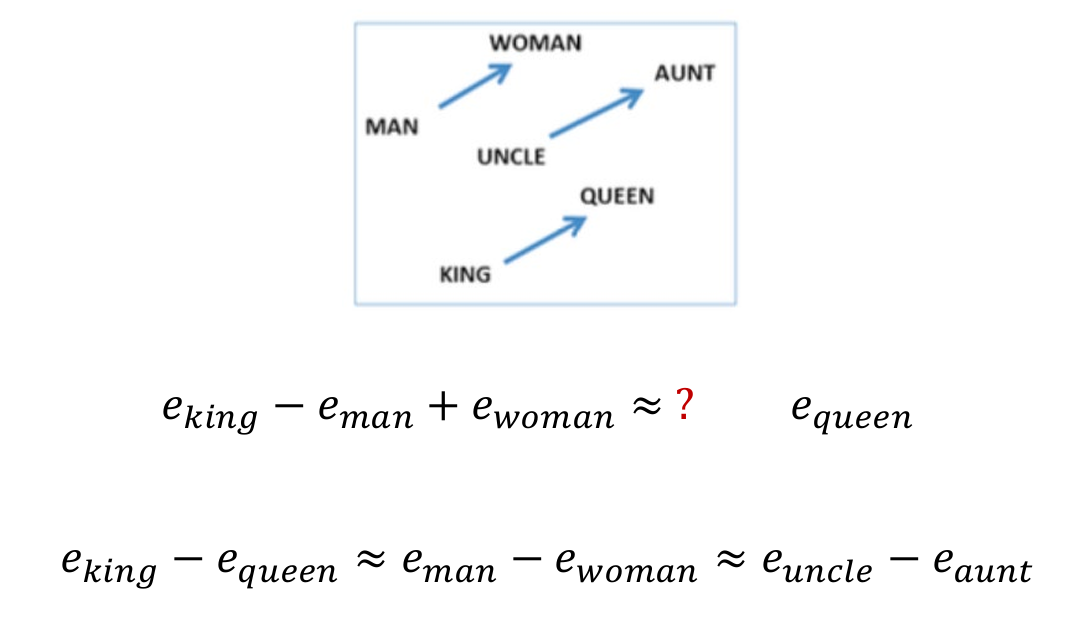
- 如 Father (David, Mike) 这一个样例知识,可首先学得 David 和 Mike 的分布式表达 (向量表达) David 和 Mike 以及谓词 Father 的分布式表达 Father
- 然后再学习一个度量函数 ψ 使得 David+Father 的结果与 Mike 很接近
即使得取值最小
一旦学习得到度量函数ψ,就可用其去判断任意两个节点之间是否具有某一关系
- 马尔可夫网络与一阶逻辑相结合的一种统计关系学习模型
- 可在一阶谓词逻辑中添加不确定性
- 其核心思想是通过为规则绑定权重的方式将一阶谓词逻辑规则中的硬性约束 ( hard constraints) 进行软化
- 一阶谓词逻辑知识库可看作是在一个可能世界的集合上建立一系列硬性规则,即如果一个世界违反了其中的某一条规则,那么这个世界的存在概率即为零
- 马尔可夫逻辑网的基本思想是让那些硬性规则有所松弛,即当一个世界违反了其中的一条规则,那么这个世界存在的可能性将降低,但并非不可能。一个世界违反的规则越少,那么这个世界存在的可能性就越大
04 概率图谱推理
概率图(probabilistic graph)
- 如果两个节点之间存在连边,则可视为这两个节点之间具有概率依赖关系而相互影响。
- 在这类图中,可用概率描述两个相连节点之间的关联,而不是假设节点之间的影响一定会百分之百发生。
- 基于概率图进行的推理被称为概率推理
概率图模型一般分为贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)两大类
- 贝叶斯网络
- 用一个有向无环图(directed acyclic graph)来表示,其用有向边来表示节点和节点之间的单向概率依赖
- 马尔可夫网络
- 表示成一个无向图的网络结构,其用无向边来表示节点和节点之间的相互概率依赖
贝叶斯网络
贝叶斯网络满足局部马尔可夫性(local Markov property):在给定一个节点的父节点的情况下,该父亲节点有条件地独立于它的非后代节点(non-descendant)
例如,对于如下网络:
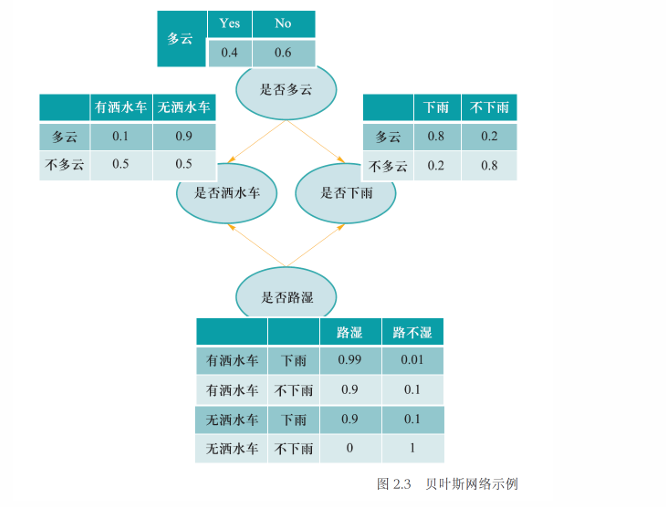
我们有:

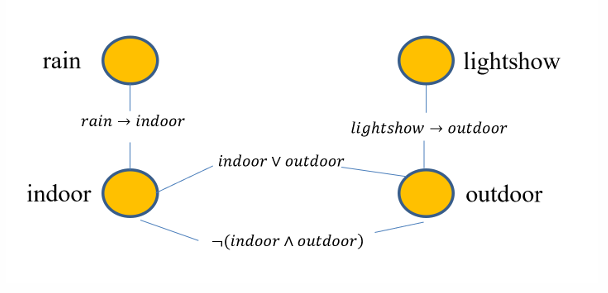
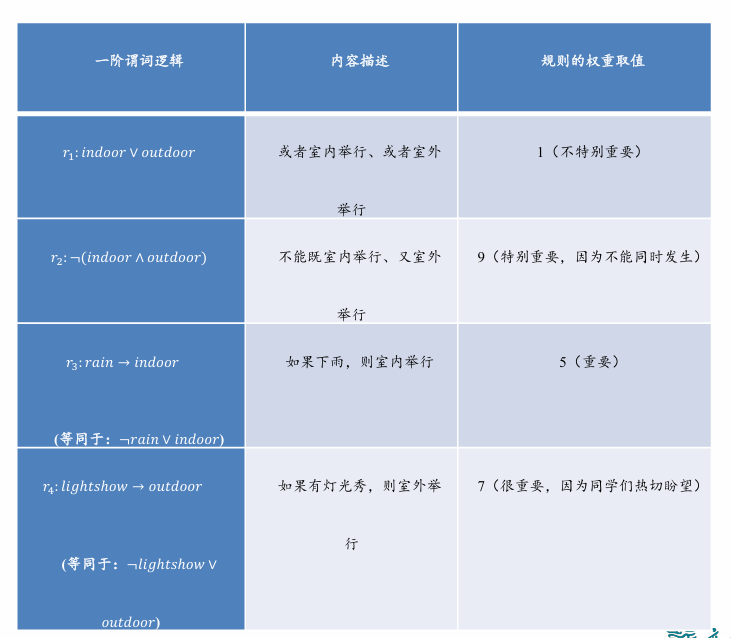
马尔可夫逻辑网络
给定一个由若干规则构成的集合,集合中每条推理规则赋予一定权重,则可如下计算某个断言 x 成立的概率:
其中

05 因果推理
如下是某组病人在是否尝试新药以后的恢复情况:不用药病人的恢复率高于用药病人的恢复率
对所有病人按照性别分组后,当比较按性别分组的两类病人的恢复率时,却发现用药病人的恢复率均高于不用药病人的恢复率
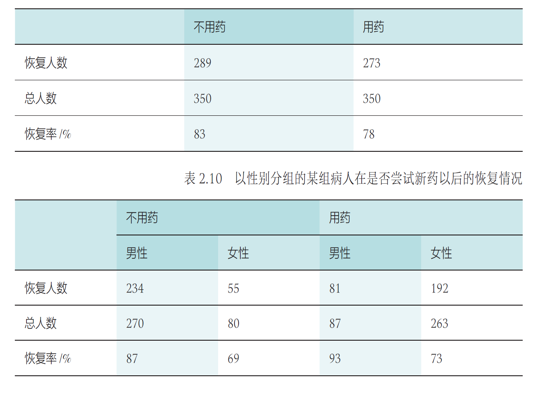
在某些情况下,忽略潜在的“第三个变量”(本例中性别就是用药与否和恢复率之外的第三个变量),可能会改变已有的结论
事实上,辛普森悖论的主要原因是因为“第三变量”导致了用药与否和恢复率之间的虚假关联
关联关系的三种来源
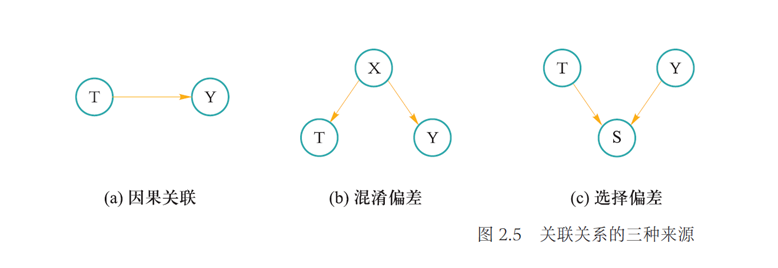
因果关联:数据中两个变量,如一个变量是另一个变量的原因,则该两变量之间存在因果关联
- 如图 (a) 所示,变量 T 是变量 Y 的原因
- "下雨会导致地面湿"
混淆关联:数据中待研究的两个变量之间存在共同的原因变量
- 如图 (b) 所示,变量 T 和 Y 存在共同的原因变量 X,即 X 是 T 的原因,同时也是 Y 的原因
- 如果忽略掉 X,那么 T 和 Y 在数据中会存在虚假关联
- "辛普森悖论":性别 (X) 会影响到患者吃药与否 (T) 以及其恢复率 (Y),如果我们忽略了性别,那么吃药与否和恢复率之间的关系就存在混淆关联
选择关联:数据中待研究的两个变量之间存在共同的结果变量
- 如图 (c) 所示,变量 T 和 Y 存在共同的结果变量 S,即 T 是 S 的原因,Y 也是 S 的原因
- 如果我们基于特定 S 的取值来选择一部分变量进行研究,那么 T 和 Y 在数据中就会存在虚假关联
- "X: 草地,Y: 狗的特征,S: 收集的图片是狗在草地上 👉 选择大量狗在草地上的图片,草地和狗就变得相关了"
两种理论框架
潜在因果框架
结构因果模型
- 因果图:有向无环图 👉 描述变量联合分布或者数据生成机制 👉 贝叶斯网络
对于有向无环图模型,模型中 d 个变量的联合概率分布:
表示节点 的父节点集合 (可以为空) - 跟前面讲贝叶斯网络时,提到给公式是一样的
例如,对于一个简单的链式图 (即有向无环图), 其联合概率分布可直接写成:
更复杂的,对于下图,有:
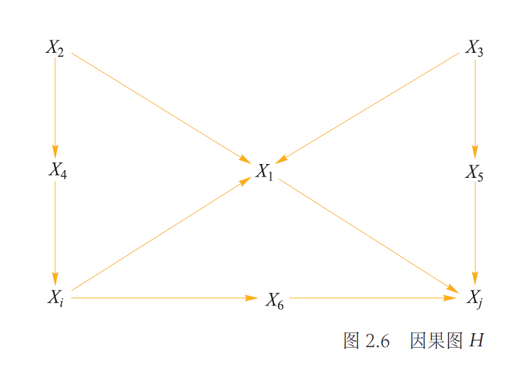
因果干预与 do 算子
干预:改变明确存在关联关系的某变量取值,研究变量取值改变对结果变量的影响
- "在已知商品价格和销售量存在关联关系的情况下,将商品价格提高一倍后,研究销售量会发生怎样的变化?"
"do"算子:计算当系统中一个变量取值发生变化、其他变量保持不变时,系统输出结果是否变化
表示的是当发现 时, 的概率;反映的是在取值为 的个体 上, 的总体分布 表示的是对 进行干预,固定其值为 时, 的概率;反映的是如果将每一个 取值都固定为 时, 的总体分布
因果效应
因果效应:给定因果图 G,PA 表示 X 的父节点集合,则
其中,z 是 PA 的具体取值
我们解释如上公式
以前面所言辛普森悖论为例,其因果图可以用下图表示:
- X 表示用药情况
- Y 表示病人的回复情况
- Z 表示性别
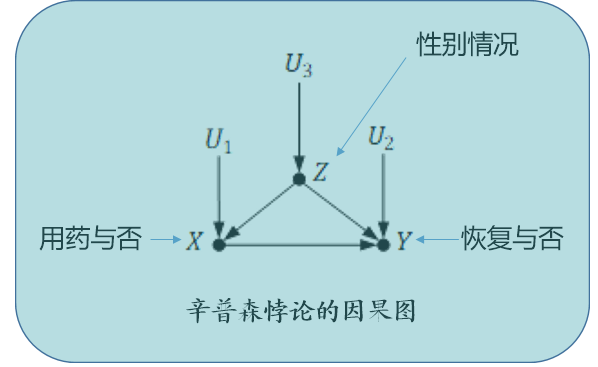
可以对病人的用药情况进行干预,来计算因果效应差:
对用药情况
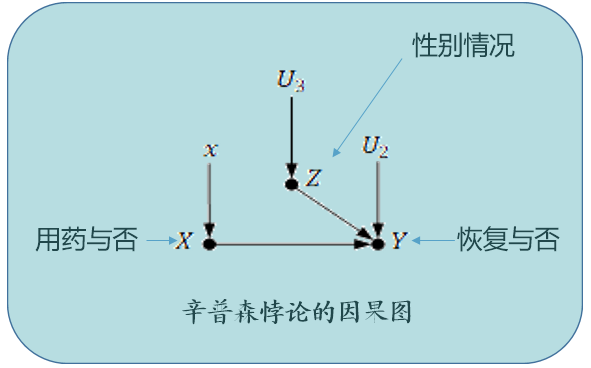
因果效应
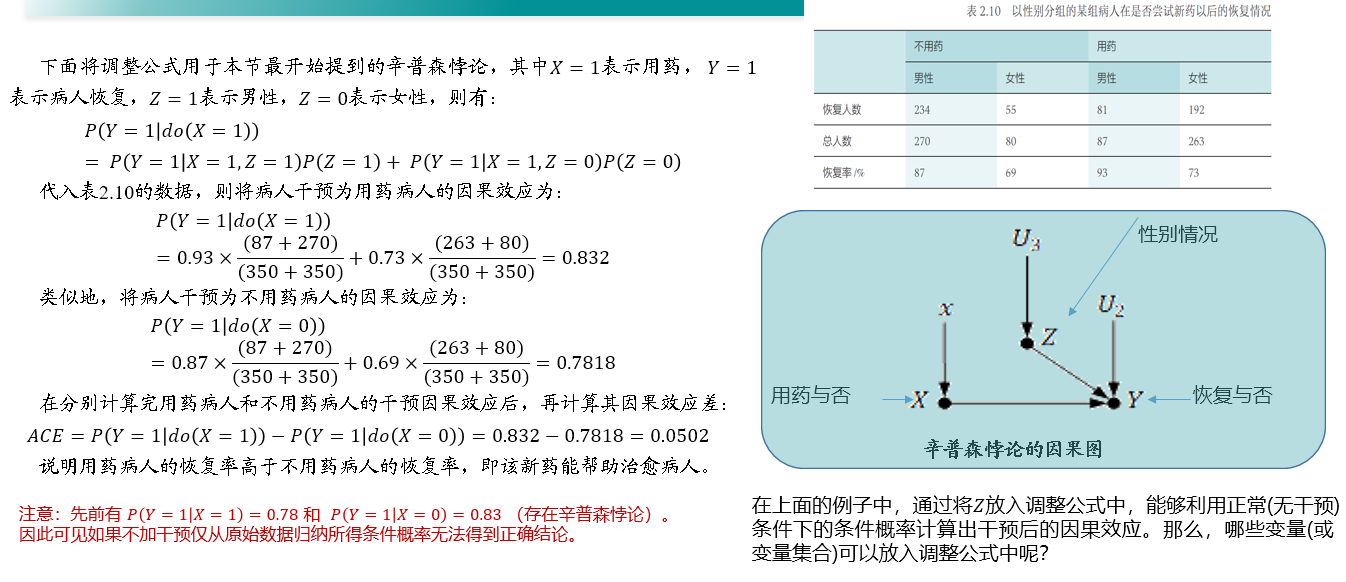
最后得到正常 (无干预) 条件下的概率表示的因果效应:
- 边缘概率
不随干预而变化,因为 Z 的取值不会因为去掉从 Z 到 X 的箭头而变化 - 条件概率
不变,因为 Y 关于 X 和 Z 的函数 并未改变 - 可用正常 (无干预) 条件下的条件概率来计算干预后的条件概率
- "调整公式" "Z 调整"
因果模型的层次化示意图
| 层次化示意图 | |||
|---|---|---|---|
| 可观测问题 | What if we see A (what is?) | $P(y\ | A)$ |
| 决策行动问题 | What if we do A (what if?) | $P(y\ | do (A))$ (如果采取 A 行为,则 y 将如何) |
| 反事实问题 | What if we did things differently (why) | $P(y'\ | A)$ (如果 A 为真,则 y′将如何) |